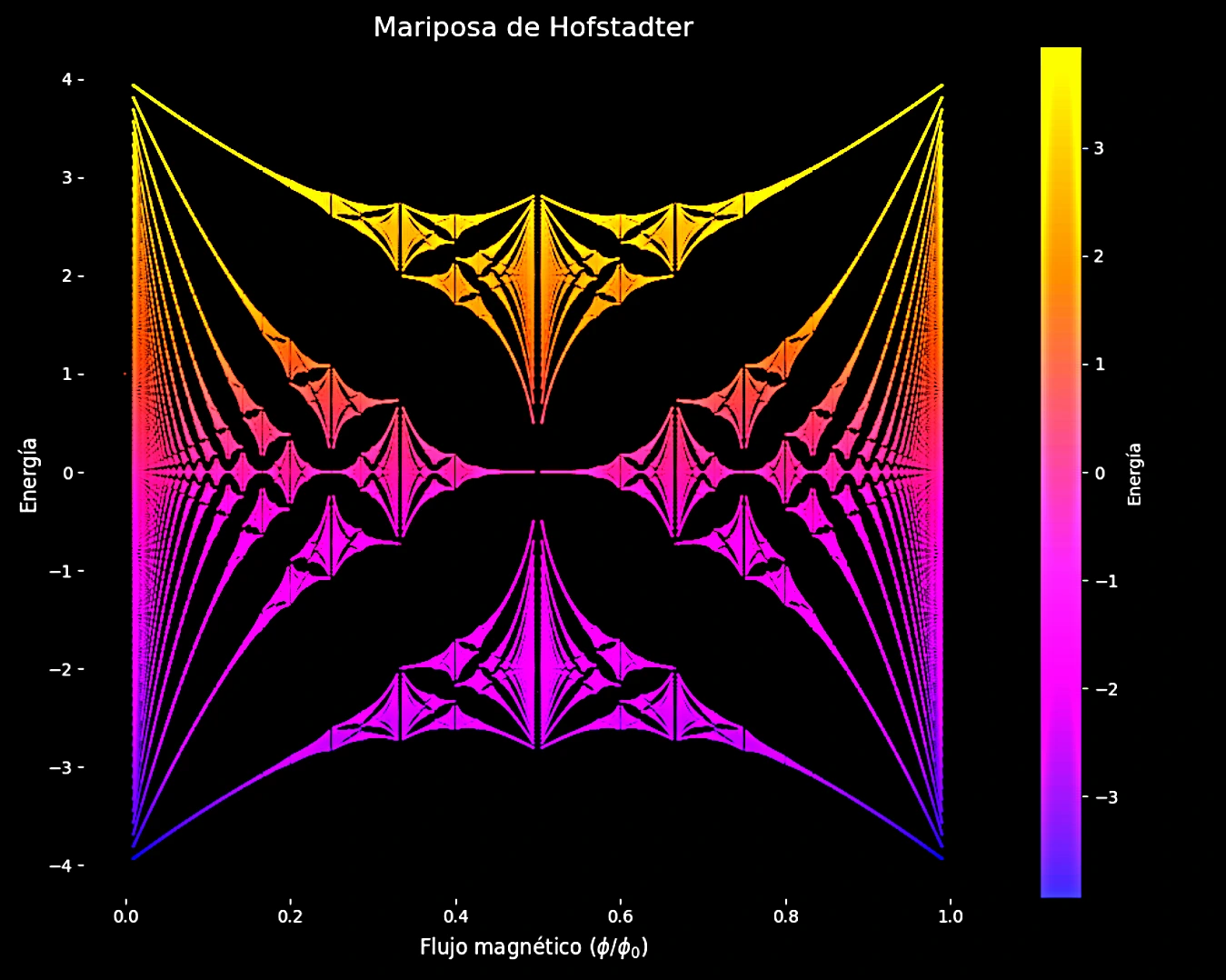
La Mariposa de Hofstadter: El Arte Cuántico del Magnetismo
- Fractales en física cuántica: La mariposa de Hofstadter es un ejemplo raro y natural de un fractal que surge directamente de la mecánica cuántica.
- Interacción entre escalas: El espectro refleja cómo la interacción entre dos escalas (la red periódica y el flujo magnético) genera estructuras increíblemente complejas.
- Matemática profunda: Este patrón conecta temas como teoría de números, geometría fractal, teoría espectral, y topología (como los invariantes de Chern).
- Aplicaciones modernas: La mariposa se ha convertido en un referente en el estudio de materiales topológicos y sistemas cuánticos como el grafeno bicapa rotado y los aislantes topológicos.
La mariposa de Hofstadter es una de las estructuras más fascinantes del mundo de la física cuántica y la matemática. No solo por su impresionante belleza visual que recuerda a las alas de una mariposa sino por el profundo entramado físico y matemático que revela sobre los electrones en campos magnéticos.
¿Qué es la Mariposa de Hofstadter?
La mariposa de Hofstadter es un diagrama fractal que representa el espectro de energía de un electrón que se mueve en un cristal bidimensional bajo la influencia de un campo magnético perpendicular. Fue descubierta en 1976 por el físico y matemático Douglas Hofstadter, quien investigaba el comportamiento de electrones en un potencial periódico (como en un cristal) cuando también están sometidos a un campo magnético. Este espectro revela cómo los niveles de energía del electrón se fragmentan de forma compleja al cambiar la razón entre el flujo magnético por celda y el flujo cuántico del electrón
El Modelo de Harper
La base matemática de esta estructura se encuentra en el llamado modelo de Harper (o modelo de casi-periódico), una ecuación en diferencias que describe cómo se propagan los electrones en una red bajo la acción de un campo magnético. En este modelo, la ecuación de Schrödinger se discretiza y da lugar a un sistema que depende de un parámetro irracional (la proporción del flujo magnético). Este sistema produce un espectro auto-similar y fractal, donde aparecen brechas (gaps) energéticos en patrones que se repiten a diferentes escalas.
¿Por qué es tan especial?
¿Dónde se ve en la Naturaleza?
Aunque inicialmente fue un fenómeno puramente teórico, en las últimas décadas la mariposa de Hofstadter ha sido observada experimentalmente en sistemas de superredes de grafeno y estructuras semiconductoras artificiales, donde se puede ajustar el campo magnético y la geometría del sistema para reproducir las condiciones ideales
Representación Visual
El gráfico clásico de la mariposa de Hofstadter tiene como eje horizontal la razón entre el flujo magnético por celda y el flujo cuántico (denotado como φ / φ0 ), y como eje vertical la energía de los electrones. El resultado es una imagen que se parece a una mariposa con múltiples alas, llena de simetrías, vacíos y estructuras que se repiten infinitamente.

Algoritmo en Python
#############################################################################
################### Sigueme en redes como: @xmistercosmox ###################
#############################################################################
import numpy as np
import matplotlib.pyplot as plt
from fractions import Fraction
# Parámetros
q_max = 200
phi_vals = []
for q in range(1, q_max + 1):
for p in range(q):
frac = Fraction(p, q)
phi_vals.append(frac)
# Removemos duplicados y ordenamos
phi_vals = sorted(set(phi_vals))
phi_plot = []
e_plot = []
colors = []
# Construcción del espectro
for frac in phi_vals:
p = frac.numerator
q = frac.denominator
h = np.zeros((q, q))
for i in range(q):
h[i, i] = 2 * np.cos(2 * np.pi * p * i / q)
h[i, (i + 1) % q] = 1
h[(i + 1) % q, i] = 1
eigs = np.linalg.eigvalsh(h)
for e in eigs:
phi = float(p) / q
phi_plot.append(phi)
e_plot.append(e)
colors.append(e)
# Graficamos
plt.figure(figsize=(10, 8), facecolor='black') # Fondo de la figura
sc = plt.scatter(phi_plot, e_plot, c=colors, cmap='plasma', s=0.15, alpha=0.8)
plt.gca().set_facecolor('black')
plt.title("Mariposa de Hofstadter", fontsize=16, color='white')
plt.xlabel(r"Flujo magnético ($\phi/\phi_0$)", fontsize=12, color='white')
plt.ylabel("Energía", fontsize=12, color='white')
plt.tick_params(colors='white')
cbar = plt.colorbar(sc)
cbar.ax.yaxis.set_tick_params(color='white')
plt.setp(plt.getp(cbar.ax.axes, 'yticklabels'), color='white')
cbar.set_label("Energía", color='white')
plt.tight_layout()
plt.show()
Resultado del algoritmo Python